Introduction

Lyman-$\alpha$ emitters and their intensity map are powerful probes of the large-scale structure. Given typically very high optical depths, scatterings with neutral hydrogen have a non-negligible impact on the observed distribution of Lyman-$\alpha$ photons. To study this in detail, we run a suit of radiative transfer (RT) simulations on the Illustris simulation and investigate two possible distortion effects arising from RT in real space as well as in redshift space for the two-point correlation function.

Context

The high optical depths and resonant nature of Lyman-$\alpha$ photons in astrophysical environments give rise to a complex radiative transfer. This can not only affect interpretation of a local galaxy’s properties, but also has an impact on the inferred cosmology/astrophysical large scale properties when Lyman-$\alpha$ emitters are used a large-scale structure tracer as in redshift surveys such as HETDEX.

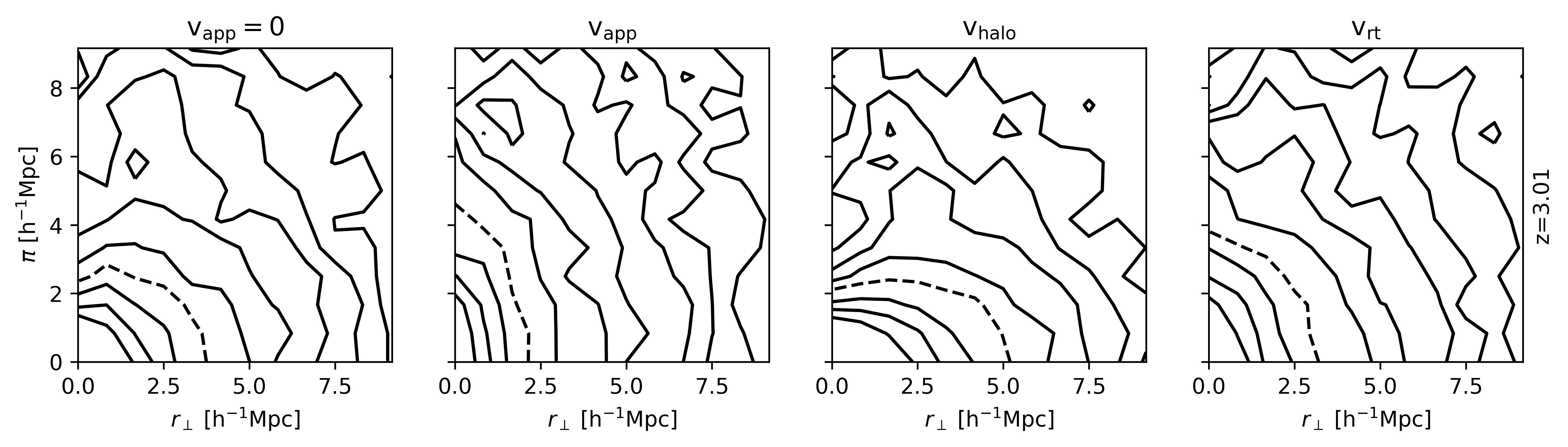
Given the correct cosmological model, we expect the dimensionally split two-point correlation (TPCF) to look the same in the line-of-sight direction $\vec{\pi}$ and perpendicular directions $\vec{r}_\perp$. As the line-of-sight position is inferred using the object’s redshift, i.e. in redshift space, it additionally has a modification from the peculiar velocity field. Commonly discussed redshift space distortions are the Fingers-of-God effect and the Kaiser effect having a characteristic impact on the TPCF:

• Kaiser Effect: Squashing along the line of sight due to coherent motion on large scales.
• Fingers-of-God Effect: Elongation due to random motion on small scales.

Additionally to these redshift space distortions, we describe and quantify two distortion effects that arise from radiative transfer as opposed to the peculiar velocity field in the classic redshift space distortions:

1. A large-scale correlation of the Lyman-$\alpha$ attenuation with the velocity gradient as first described in ( Zheng et al., 2010) and possibly detected in ( Croft et al., 2016).
2. Changes in the small-scale environment give rise to changes in the observed spectra, which translates to an additional uncertainty in the inferred emitters’ redshift space position.

We quantify and describe these effects using full radiative transfer simulations on top of the state-of-the-art cosmological simulation project Illustris.

Simulation Setup

Illustris

Illustris is a set of cosmological simulations coupling dark matter and a variety of baryon physics with a box size of up to $75\ $Mpc/h and a resolution of roughly $1\ $ckpc run using the AREPO code on a Voronoi tesselation ( Vogelsberger et al., 2014, Nelson et al., 2015). For the radiative transfer, we interpolate this tesselation onto an octet tree with resolutions down to $3.3\ $ckpc.

Radiative Transfer

Using the publicly available Illustris data, we run the Lyman-$\alpha$ radiative transfer as a Monte Carlo postprocessing step. Lyman-$\alpha$ luminosities are assigned proportionally to the star formation rate and placed into each (sub-)halo’s center. The initial spectrum arising from the ISM is simplified as a Gaussian with a Doppler width according to the halo’s virial temperature.

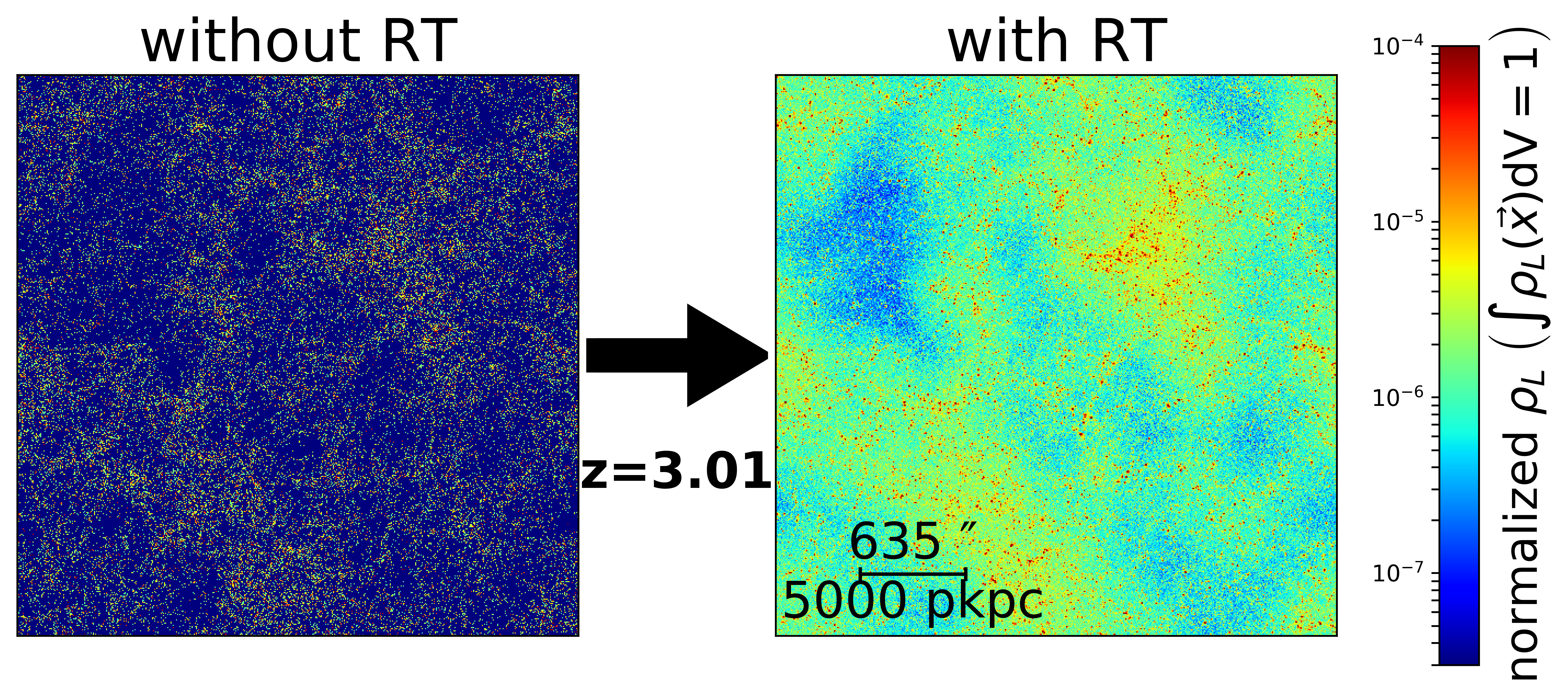
As we focus on the resulting galaxy clustering here, we further reduce the resulting intensity maps from radiative transfer to obtain galaxy catalogs. For this, we employ a range of detection algorithms finding similar outcomes independent of used choice. These algorithms do not only allow to infer positions, but also apparent luminosities $L_\mathrm{app}$ as opposed to the intrinsic ones $L_\mathrm{int}$. We will compute the ratio $\varepsilon = \frac{L_\mathrm{app}}{L_\mathrm{int}}$ to check for correlations with the large-scale structure. This quantity should capture part of the radiative transfer both in terms of line-of-sight attenuation and spatial diffusion.

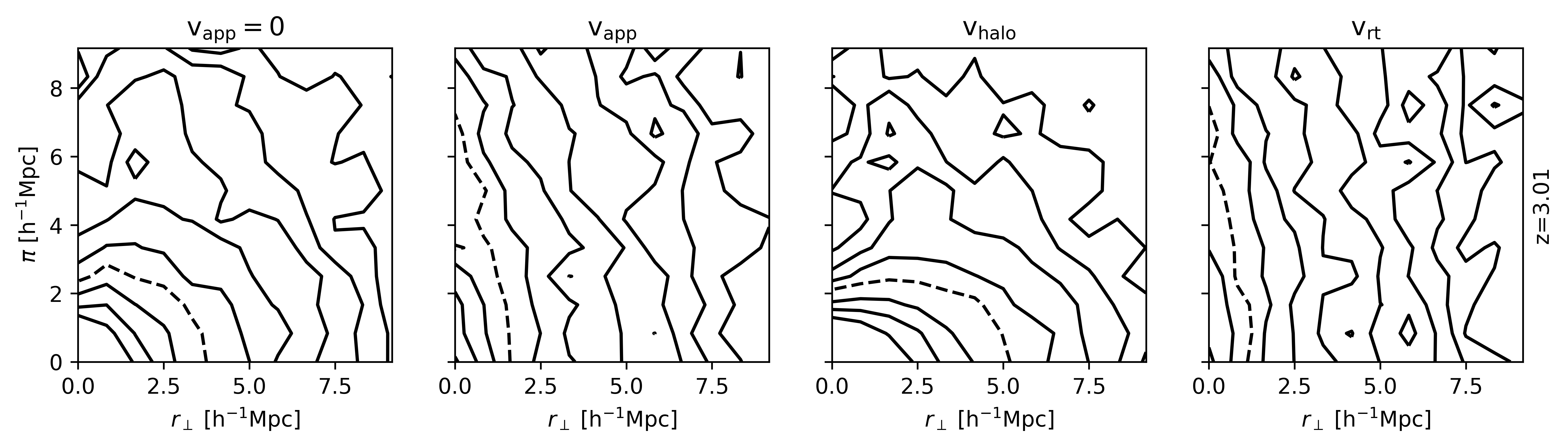
RT Effect #1

For a sample of Lyman-$\alpha$ emitters with some minimal flux threshold detected, a selection effect exists in real space causing an elongation in $\vec{\pi}$ and squashing in $\vec{r}_{\perp}$ direction. Mathematically, this is somewhat similar to the Kaiser effect. This effect can be attributed to the Lyman-$\alpha$ optical depth and spatial diffusion being correlated with the large-scale structure. In the constructed LAE catalogs, we find:

These correlations and implied distortions were first found and derived in ( Zheng et al., 2010, Zheng et al., 2011). ( Wyithe and Dijkstra, 2011) give a simplified but analytic description of these correlations with the IGM attenuation. A follow-up by ( Behrens et al., 2013) could not reproduce this effect, so that the strength of this effect was unclear. The Lyman-$\alpha$ observations in ( Croft et al., 2016) show an elongation along the line of sight with a possible explanation given by this radiative transfer distortion effect.

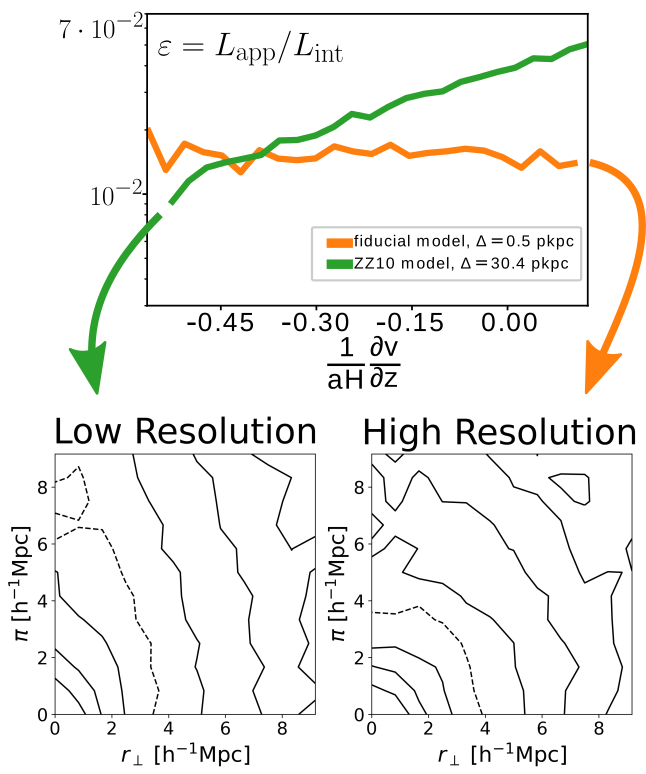
In our simulations, we do not find the distortion effect described in ( Zheng et al., 2011). However, we are able to reproduce their results by adopting two of their assumptions:

1. Reduction of the hydrodynamic resolution from $0.5\ $pkpc to $30.4\ $pkpc (at $z=5.85$) by smoothing the Illustris’ snapshots prior to radiative transfer.
2. Adopting a shallower mass-to-luminosity relation. Prior to this, we rely on the local star formation rate to determine the Lyman-$\alpha$ luminosity for a given initial mass function integrating the ionizing flux. This amounts to a relation with significant scatter but averaging $L\sim M^{1.7}$, while prior publication sets a fixed one-to-one relationship with $L\sim M$.

As our original setup is physically better motivated, we argue prior findings are a numerical artifact. Furthermore, we can motivate these assumptions’ impact on the resulting large-scale structure correlations:

1. A lower hydrodynamic resolution decreases the optical depth around the ISM, which causes the resulting spectrum to be aligned closer to the line center as frequency diffusion is reduced. Photons near the line-center are strongly susceptible to the large-scale environment, particularly at very high redshifts. For more information, see here. Thus, a lower resolution will enhance large-scale correlations of the Lyman-$\alpha$ attenuation.
2. Changing the emitter model to a shallower $L(M)$ relation will add larger weights to low mass emitters, which have a spectrum closer to the line center and thus being more susceptible.

Interestingly, at lower redshifts ($z\lesssim 4.01$) even after artificially degrading the resolution, we do not find an anisotropic distortion effect as at $z=5.85$. This can be partially attributed to the decreasing physical neutral hydrogen density in the IGM. Based on our results, we do not expect this distortion to occur in the HETDEX redshift survey.

RT Effect #2

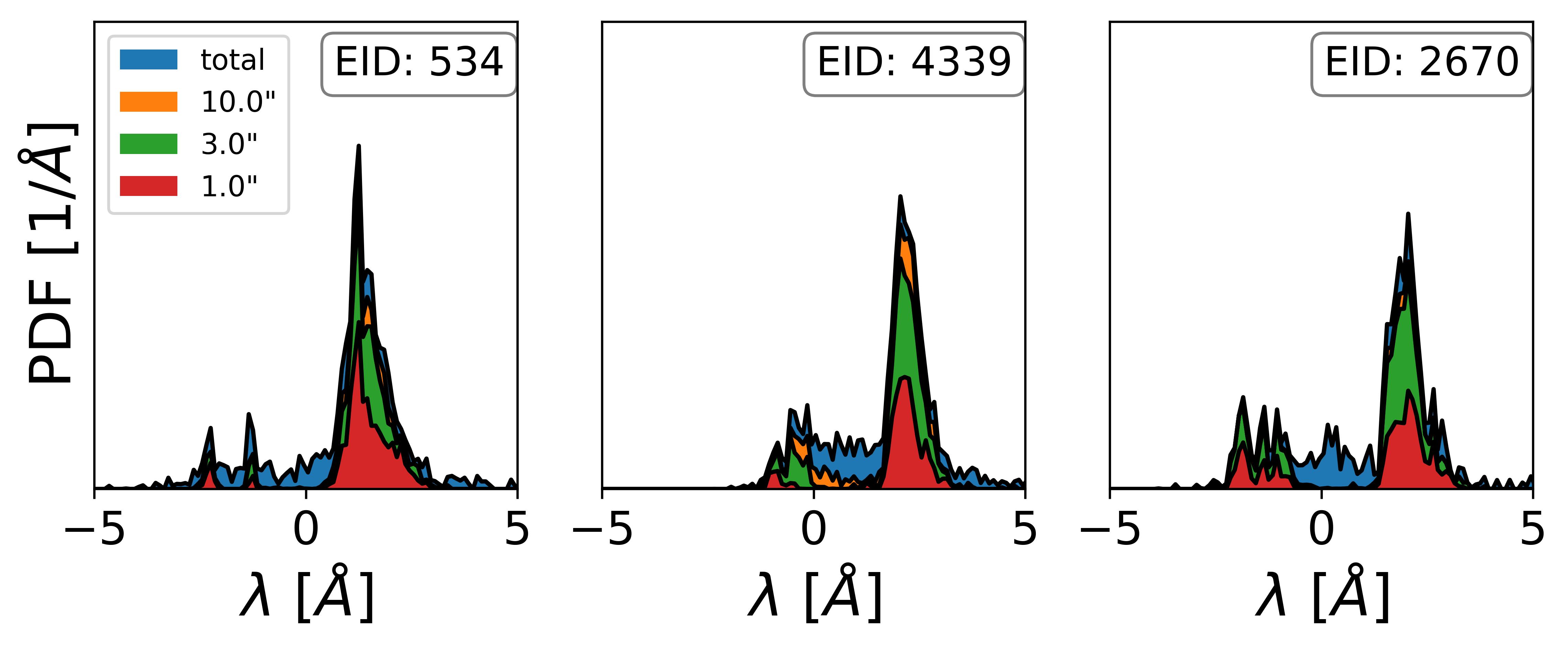
Individual Lyman-$\alpha$ emitters show varying spectra, mostly based on their small-scale environment. Locating the emitters by their (global) peak’s position results in an elongation along $\vec{\pi}$ in redshift space of the TPCF similar to the Fingers-of-God effect.

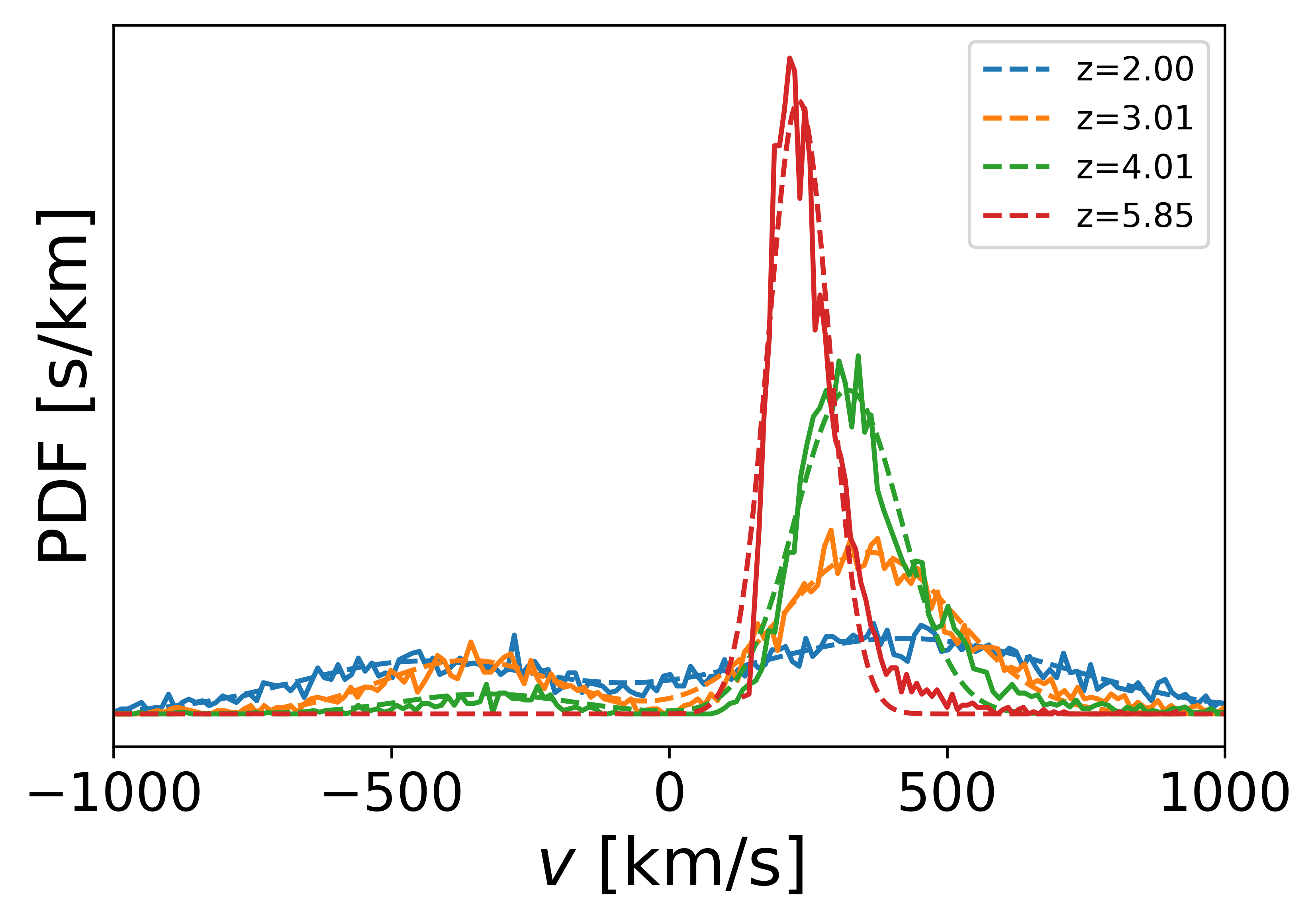
The shape and strength of this second distortion strongly depend on the chosen detection algorithm, which can be supplemented by further information about the LAE’s properties to minimize its effect. In order to give a transparent account of its impact, we choose to stick with a simple algorithm, in which we identify the emitter’s position by its spectral global peak for a fixed circular aperture. After obtaining individual spectra for each emitter, we compute the probability distribution of the apparent velocities of these emitters by their global peaks. Note that this probability distribution depends on the chosen lower mass/ luminosity cut.

As the effect seems similar to the Fingers-of-God effect, we similarly approach this problem using a moment-based decomposition of the power damping term, but find no convergence due to the extended wings of the radiative velocity distribution.

At low redshifts, most of the massive emitters show a characteristic double peak spectrum in our simulations, but their abundance is inconsistent with observations, where most emitters appear to be single peaked. Therefore the found probability distribution of peaks is too broad as to be consistent with observations. Just as for the first distortion effect, the small-scale spectral modeling shows to be crucial for a accurate account of this effect. In order to give a more realistic estimate on this distortion, we also compute the probability distribution arising from the red peaks only (correctly accounting for the peculiar velocity), see here. While this is not fully self-consistent, for which the small-scale spectral modeling would need to be improved instead of ignoring the resulting blue peaks, this should give a rough estimate of the expected effect.

In any case, the found distortion is significant with typical scale length in the order of Mpc. Validating these results with ( Zheng et al., 2011), we confirm that this effect was not present due to their modeling deficiencies and high redshift.

Conclusions

Lyman-alpha emitters are a theoretically challenging large-scale structure tracer. Performing full radiative transfer on hydrodynamic simulations, we quantity the strengths of two possible distortion effects:

• RT Distortion #1:
• Elongation effect due to coherent attenuation on large scales.
• For chosen setup, this effect only shows up when decreasing the hydrodynamic resolution, making it a numerical artifact.
• Not reproduced for $z\le 4$ even with decreased resolution $\rightarrow$ Good news for ground-based Lyman-$\alpha$ surveys such as HETDEX.
• RT Distortion #2:
• Elongation due to random spectrum on small scales.
• Despite lack of large-scale correlations, modeling of tricky due to non-trivial probability distribution.

Appendix

IGM Attenuation

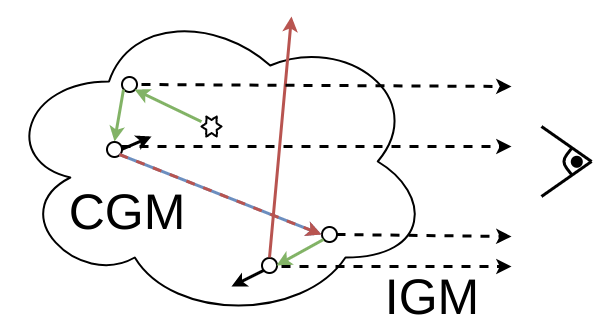
For the attenuation in the IGM with a uniform background, we expect a proportionality with $\frac{dv_z}{dz}$ quantifying how ‘quickly’ an emitted photon crosses the center of the line profile, also see ( Wyithe and Dijkstra, 2011). The figure above visualizes this for an individual emitter where photons having an initial frequency $\Delta\lambda$ (in the cosmological restframe) will eventually cross the line center and the integrated attenuation is the higher the flatter $\frac{dv_z}{dz}$. However, this statement is oversimplified as there is a strong dependence on the initial frequency. If an initial photon is sufficiently red ($\Delta\lambda\gg0$), it will never be shifted into the line center by the cosmological redshift. Far from the line-center in the red wing, the attenuation is negligible and therefore there is no noticeable dependency of the overall observed flux on the velocity gradient for red photons. Only photons close to the line center or in the blue wing have sufficient optical depth to contribute to a large-scale structure correlation. Adding an inhomogeneous density field further complicates this: While a higher velocity gradient will help photons to pass the line center faster, it will also make them hit the line-center earlier, where the density should be higher, which should increase the attenuation. Therefore the resulting overall correlation with the velocity gradient is not trivial to calculate. Adding the peculiar velocity structure introduces another complication as small-scale velocity fluctuations can alter the attenuation dependency.

Conservative Spectra

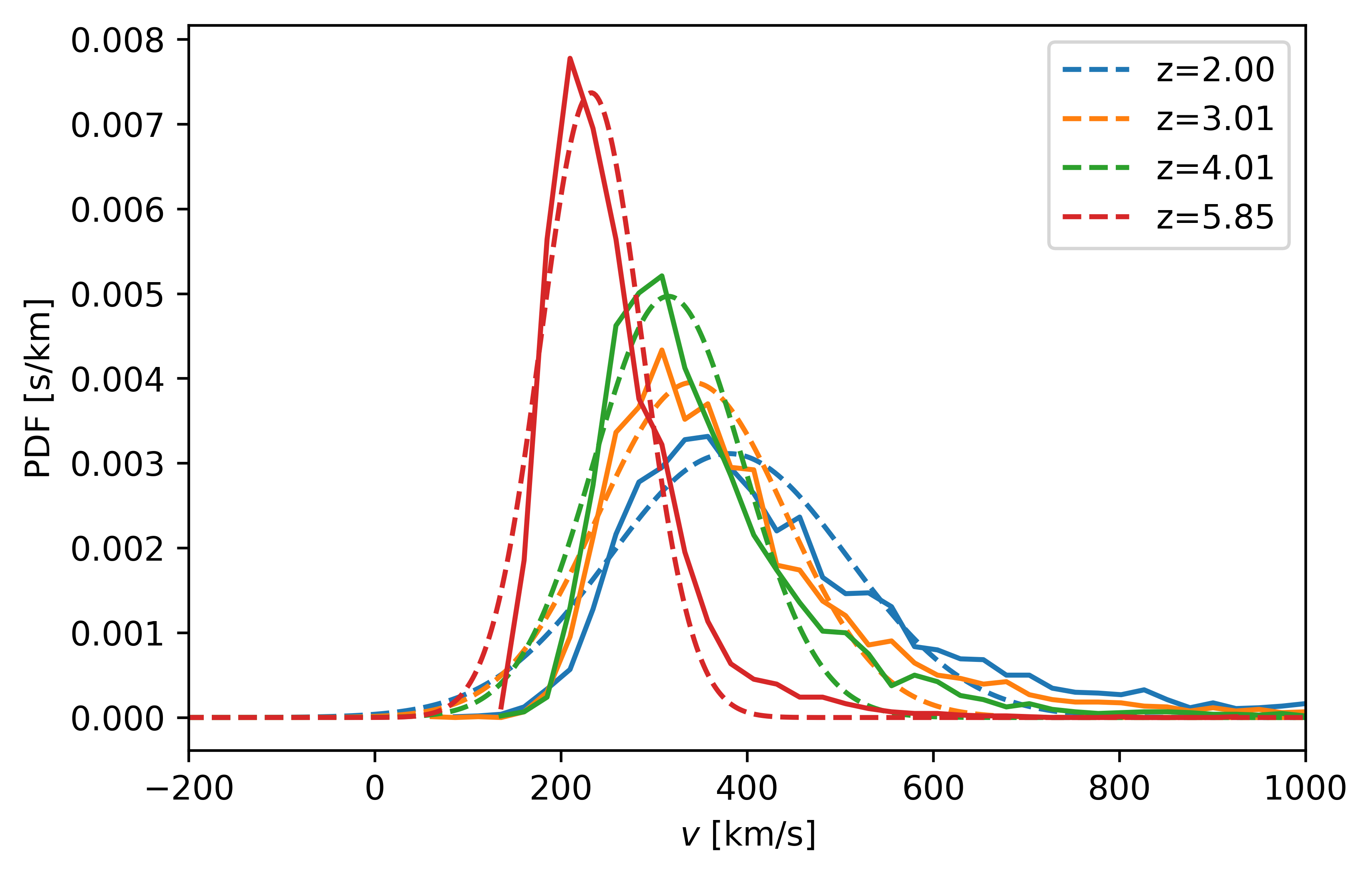
Even at low redshift, where IGM attenuation for Lyman-$\alpha$ is low, spectra from observations do not show significant amounts of emitters having a dominant blue peak. This is contradicting our results, likely arising from insufficient small-scale modeling in the setup. As such modeling can be complex, a short-term hack in order to get a more realistic estimate for the distortion’s magnitude is to only allow detection of red peaks rather than the global maximum.

`